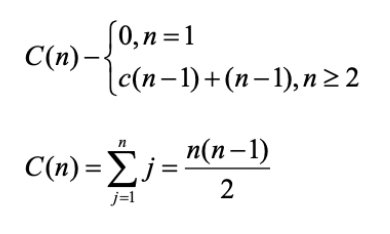Chap5 归纳法

Posted Apr 4, 2025

By floyd white

16 min read

Chap5 归纳法

4.2

用迭代算法计算斐波那契数

long long Fibonacci(int n)
{
	if (n == 0)
		return 0;
	else if (n == 1)
		return 1;
	long long a = 0;
	long long b = 1;
	long long c = 1;
	while (n - 2)
	{
		a = b;
		b = c;
		c = a + b;
		n--;
	}
	return c;
}

4.3

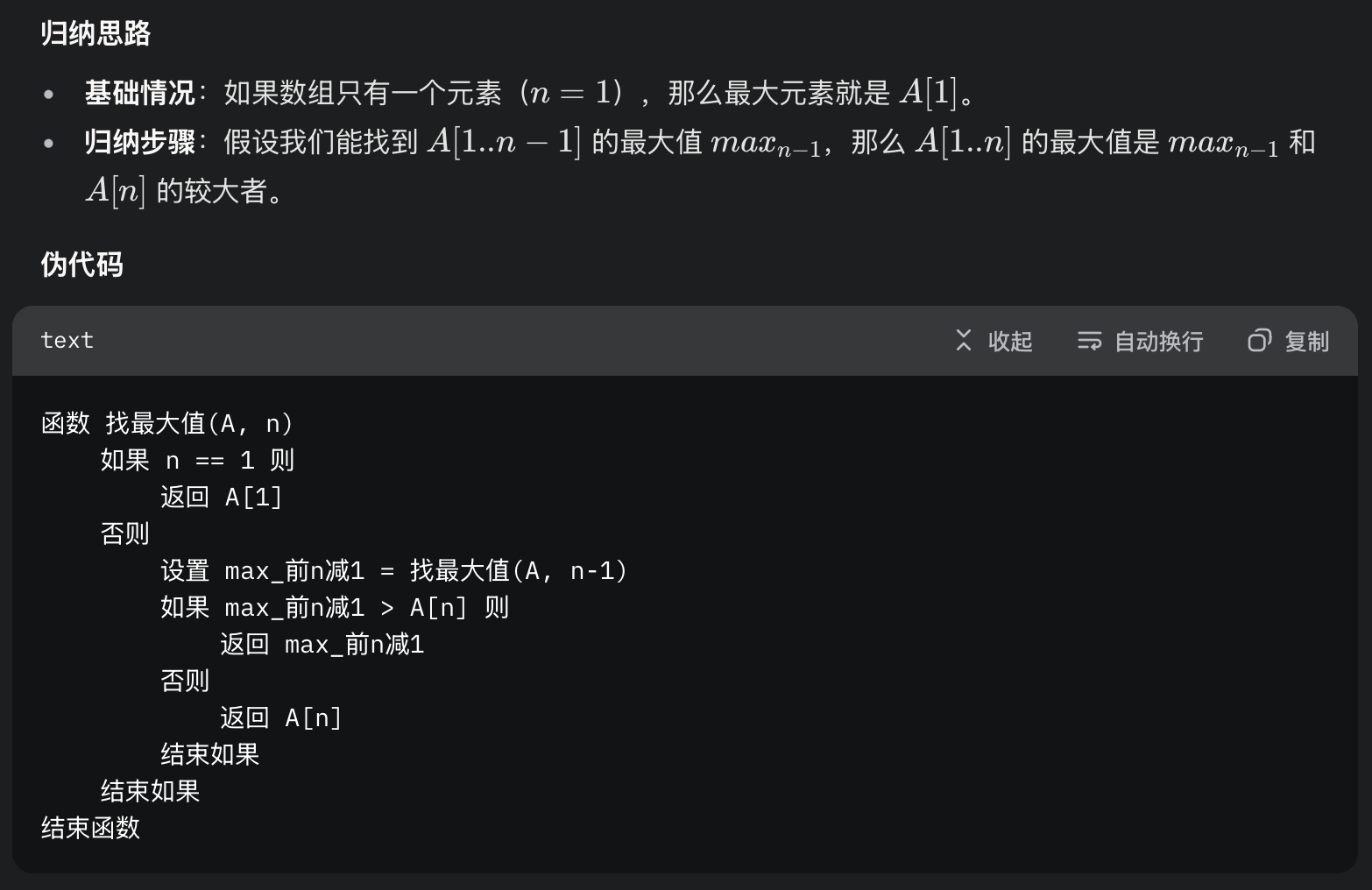
用归纳法开发一个递归算法，找出序列A[1..n] 中的最大元素

4.4

用归纳法开发一个递归算法，计算序列A[1..n] 中的平均值

4.5

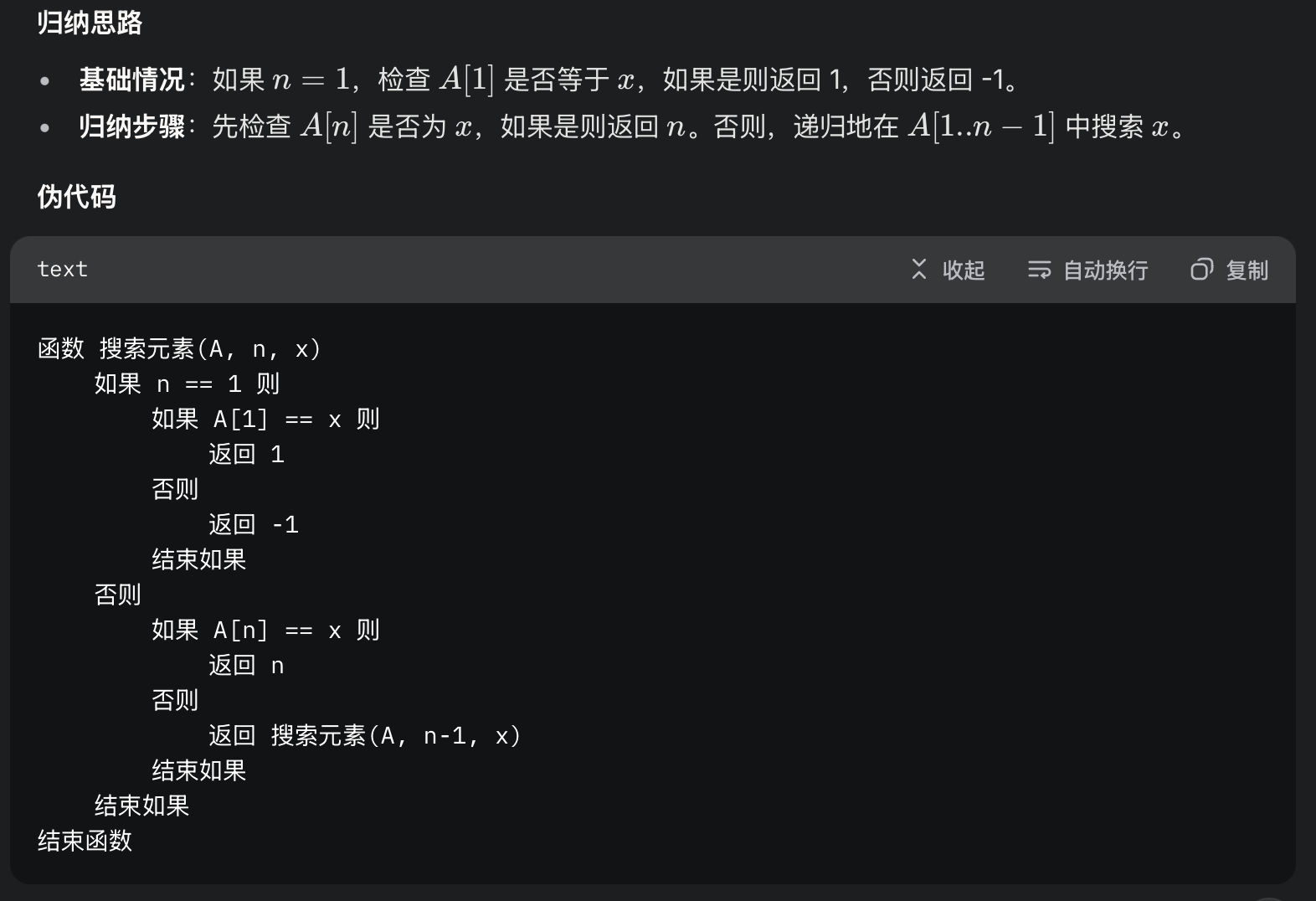
用归纳法开发一个递归算法，在序列A[1..n] 中搜寻元素x

4.6

计算SELECTIONSORT的运行时间

见书P91

递归版本的选择排序比起P8的迭代版选择排序，只是把最外层的for循环改成了递归sort(i+1)而已
$c(n-1)+(n-1)$ 代表n-1次元素比较次数加上对A[2…n]排序的比较次数

4.7

实现选择排序（SELECTIONSORT）、插入排序（INSERTIONSORT）和冒泡排序（BUBBLESORT）的递归版本
—

4.6 选择排序（递归版）

代码

  
// 递归实现选择排序
void selectionSort(vector<int>& A, int start, int n) {
    // 基础情况：如果 start 到达 n-1，只剩一个或没有元素，无需排序
    if (start >= n - 1) {
        return;
    }

    // 找到从 start 到末尾的最小元素索引
    int min_idx = start;
    for (int i = start + 1; i < n; i++) {
        if (A[i] < A[min_idx]) {
            min_idx = i;
        }
    }

    // 交换 start 位置和最小元素位置
    swap(A[start], A[min_idx]);

    // 递归处理从 start+1 到末尾的部分
    selectionSort(A, start + 1, n);
}

说明

start 表示当前未排序部分的起始位置，n 是数组长度。
每次递归找到最小元素，放到 start 位置，然后递归处理剩余部分。

4.7 插入排序（递归版）

代码

  
// 递归实现插入排序
void insertionSort(vector<int>& A, int n) {
    // 基础情况：如果 n <= 1，只有一个或没有元素，无需排序
    if (n <= 1) {
        return;
    }

    // 递归排序前 n-1 个元素
    insertionSort(A, n - 1);

    // 取最后一个元素，插入到前 n-1 个已排序部分的正确位置
    int key = A[n - 1];
    int j = n - 2;

    // 向后移动大于 key 的元素
    while (j >= 0 && A[j] > key) {
        A[j + 1] = A[j];
        j--;
    }

    // 插入 key 到正确位置
    A[j + 1] = key;
}

说明

递归排序前 ( n-1 ) 个元素。
取最后一个元素 key，通过移动元素将其插入到已排序部分的正确位置。

4.8 冒泡排序(递归版)

代码

  
// 递归实现冒泡排序
void bubbleSort(vector<int>& A, int n) {
    // 基础情况：如果 n <= 1，只有一个或没有元素，无需排序
    if (n <= 1) {
        return;
    }

    // 一轮冒泡，将最大元素放到末尾
    for (int i = 0; i < n - 1; i++) {
        if (A[i] > A[i + 1]) {
            swap(A[i], A[i + 1]);
        }
    }

    // 递归处理前 n-1 个元素
    bubbleSort(A, n - 1);
}

说明

每轮冒泡将最大元素放到末尾。
递归处理前 ( n-1 ) 个元素，直到数组完全排序。

规律

可以看出，这三个排序算法的递归版和迭代版的区别就是：用递归调用自身的方式，代替了迭代法的外层for循环。

4.9 多数元素算法的迭代版本

  
// 实现 candidate(m) 的迭代版本
int candidate(const vector<int>& A, int m) {
    int j = m;              // 从索引 m 开始
    int c = A[m];           // 初始候选元素
    int count = 1;          // 初始计数为 1

    // 遍历直到 count 变为 0 或到达数组末尾
    while (j < A.size() && count > 0) {
        j++;
        if (j < A.size()) {
            if (A[j] == c) {
                count++;    // 遇到相同元素，计数加 1
            } else {
                count--;    // 遇到不同元素，计数减 1
            }
        }
    }

    // 如果遍历到末尾，返回当前候选元素
    if (j == A.size()) {
        return c;
    }
    // 否则递归调用 candidate(j+1)
    return candidate(A, j + 1);
}

// 实现 MAJORITY 算法的迭代版本
int majority(const vector<int>& A) {
    // 步骤 1: 找到候选元素
    int c = candidate(A, 0);
    int count = 0;

    // 步骤 2: 统计候选元素 c 的出现次数
    for (int j = 0; j < A.size(); j++) {
        if (A[j] == c) {
            count++;
        }
    }

    // 步骤 3: 验证是否为众数
    if (count > A.size() / 2) {
        return c;  // 如果出现次数超过 n/2，返回 c
    } else {
        return -1; // 否则返回 -1 表示“none”
    }
}

4.10 展示MAJORITY在给定数组上的运行过程

好的，我会用中文解答题目 4.9 和 4.10，分别实现算法 MAJORITY 的迭代版本，并展示其在给定数组上的运行过程。我会直接用 C++ 代码实现，并详细解释每一步。

4.9 给出算法 MAJORITY 的迭代版本

算法 MAJORITY 简介

算法 MAJORITY 用于在一个数组 ( A[1..n] ) 中寻找“众数”（majority element），即出现次数超过 ( \lfloor n/2 \rfloor ) 的元素。如果不存在这样的元素，则返回“none”。

算法的核心是 Boyer-Moore 投票算法（Boyer-Moore Voting Algorithm），其思路是：

维护一个候选元素 ( c ) 和计数器 ( count )。
遍历数组，遇到与 ( c ) 相同的元素时 ( count++ )，否则 ( count– )。
如果 ( count ) 变为 0，则选择当前元素作为新的候选元素。
最后验证候选元素是否真的是众数。

C++ 代码实现

  
#include <vector>
using namespace std;

// 实现 candidate(m) 的迭代版本
int candidate(const vector<int>& A, int m) {
    int j = m;              // 从索引 m 开始
    int c = A[m];           // 初始候选元素
    int count = 1;          // 初始计数为 1

    // 遍历直到 count 变为 0 或到达数组末尾
    while (j < A.size() && count > 0) {
        j++;
        if (j < A.size()) {
            if (A[j] == c) {
                count++;    // 遇到相同元素，计数加 1
            } else {
                count--;    // 遇到不同元素，计数减 1
            }
        }
    }

    // 如果遍历到末尾，返回当前候选元素
    if (j == A.size()) {
        return c;
    }
    // 否则递归调用 candidate(j+1)
    return candidate(A, j + 1);
}

// 实现 MAJORITY 算法的迭代版本
int majority(const vector<int>& A) {
    // 步骤 1: 找到候选元素
    int c = candidate(A, 0);
    int count = 0;

    // 步骤 2: 统计候选元素 c 的出现次数
    for (int j = 0; j < A.size(); j++) {
        if (A[j] == c) {
            count++;
        }
    }

    // 步骤 3: 验证是否为众数
    if (count > A.size() / 2) {
        return c;  // 如果出现次数超过 n/2，返回 c
    } else {
        return -1; // 否则返回 -1 表示“none”
    }
}

说明

candidate 函数通过迭代实现，找到一个可能的候选元素。
majority 函数调用 candidate 找到候选元素，然后验证其出现次数是否超过 ( \lfloor n/2 \rfloor )。
返回值用 -1 表示“none”，如果有众数则返回该元素。

复杂度

时间复杂度：( O(n) )，需要两次遍历数组。
空间复杂度：( O(1) )，只用了常数额外空间。

4.10 展示算法 MAJORITY 在给定数组上的运行过程

我们需要对以下三个数组运行 MAJORITY 算法，并展示每一步：

(a) ( [5, 7, 5, 4, 5] )
(b) ( [5, 7, 5, 4, 8] )
(c) ( [2, 4, 1, 4, 4, 4, 6, 4] )

(a) 数组 ( [5, 7, 5, 4, 5] )

步骤 1: 找到候选元素

初始：( c = 5 ), ( count = 1 ), ( j = 0 )
( j = 1 ), ( A[1] = 7 \neq 5 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 7 ), ( count = 1 ), ( j = 2 )
( j = 2 ), ( A[2] = 5 \neq 7 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 5 ), ( count = 1 ), ( j = 3 )
( j = 3 ), ( A[3] = 4 \neq 5 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 4 ), ( count = 1 ), ( j = 4 )
( j = 4 ), ( A[4] = 5 \neq 4 ), ( count = 1 - 1 = 0 )
( count = 0 )，但 ( j = 4 ) 是最后一个元素，结束循环
候选元素 ( c = 5 )（因为最后一次更新后 ( c ) 变为 5）

步骤 2: 统计候选元素 ( c = 5 ) 的出现次数

遍历数组：( [5, 7, 5, 4, 5] )
( 5 ) 出现 3 次，( count = 3 )

步骤 3: 验证

数组长度 ( n = 5 )，( \lfloor n/2 \rfloor = 2 )
( count = 3 > 2 )，所以 ( 5 ) 是众数

结果：返回 ( 5 )

(b) 数组 ( [5, 7, 5, 4, 8] )

步骤 1: 找到候选元素

初始：( c = 5 ), ( count = 1 ), ( j = 0 )
( j = 1 ), ( A[1] = 7 \neq 5 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 7 ), ( count = 1 ), ( j = 2 )
( j = 2 ), ( A[2] = 5 \neq 7 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 5 ), ( count = 1 ), ( j = 3 )
( j = 3 ), ( A[3] = 4 \neq 5 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 4 ), ( count = 1 ), ( j = 4 )
( j = 4 ), ( A[4] = 8 \neq 4 ), ( count = 1 - 1 = 0 )
( count = 0 )，但 ( j = 4 ) 是最后一个元素，结束循环
候选元素 ( c = 8 )（因为最后一次更新后 ( c ) 变为 8）

步骤 2: 统计候选元素 ( c = 8 ) 的出现次数

遍历数组：( [5, 7, 5, 4, 8] )
( 8 ) 出现 1 次，( count = 1 )

步骤 3: 验证

数组长度 ( n = 5 )，( \lfloor n/2 \rfloor = 2 )
( count = 1 \leq 2 )，所以没有众数

结果：返回 -1（表示“none”）

(c) 数组 ( [2, 4, 1, 4, 4, 4, 6, 4] )

步骤 1: 找到候选元素

初始：( c = 2 ), ( count = 1 ), ( j = 0 )
( j = 1 ), ( A[1] = 4 \neq 2 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 4 ), ( count = 1 ), ( j = 2 )
( j = 2 ), ( A[2] = 1 \neq 4 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 1 ), ( count = 1 ), ( j = 3 )
( j = 3 ), ( A[3] = 4 \neq 1 ), ( count = 1 - 1 = 0 )
( count = 0 )，更新候选元素：( c = 4 ), ( count = 1 ), ( j = 4 )
( j = 4 ), ( A[4] = 4 = c ), ( count = 1 + 1 = 2 )
( j = 5 ), ( A[5] = 4 = c ), ( count = 2 + 1 = 3 )
( j = 6 ), ( A[6] = 6 \neq 4 ), ( count = 3 - 1 = 2 )
( j = 7 ), ( A[7] = 4 = c ), ( count = 2 + 1 = 3 )
遍历结束，候选元素 ( c = 4 )

步骤 2: 统计候选元素 ( c = 4 ) 的出现次数

遍历数组：( [2, 4, 1, 4, 4, 4, 6, 4] )
( 4 ) 出现 5 次，( count = 5 )

步骤 3: 验证

数组长度 ( n = 8 )，( \lfloor n/2 \rfloor = 4 )
( count = 5 > 4 )，所以 ( 4 ) 是众数

结果：返回 ( 4 )

Algorithm Design, Solutions

solution

This post is licensed under CC BY 4.0 by the author.

4.2

4.3

4.4

4.5

4.6

4.7

4.6 选择排序（递归版）

代码

说明

4.7 插入排序（递归版）

代码

说明

4.8 冒泡排序(递归版)

代码

说明

规律

4.9 多数元素算法的迭代版本

4.10 展示MAJORITY在给定数组上的运行过程

4.9 给出算法 MAJORITY 的迭代版本

算法 MAJORITY 简介

C++ 代码实现

说明

复杂度

4.10 展示算法 MAJORITY 在给定数组上的运行过程

(a) 数组 ( [5, 7, 5, 4, 5] )

(b) 数组 ( [5, 7, 5, 4, 8] )

(c) 数组 ( [2, 4, 1, 4, 4, 4, 6, 4] )

Trending Tags