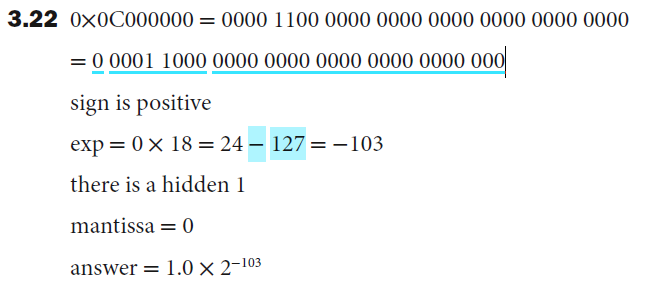chap3_solutions

提纲

1. 3.1~3.11这些题很容易迷糊，有时间多做几遍

3.1~3.5

---

• ”n位m进制数“：指的是这个数转换为二进制的话有n位、但这个数本身是一个m进制数！
• ”以符号-数值形式存储“：把这个数的二进制数”当成”符号-数值形式来看
• ”以二进制补码形式存储“：把这个数的二进制数”当成”二进制补码形式来看
• ”4365-3412用无符号12位八进制数表示是什么？“
  4365和3412这两个数就是八进制数，它们转换为二进制就是12位的。它们相减的差也是一个12位八进制数，求这个差值的八进制表示；
  所以解答过程就是：先把4365和3412转化为10进制数，然后计算它们的差值的十进制值，再把这个十进制值转化为八进制即可；
• 注意，像4365这样的八进制数转化为十进制数的方法是：
  
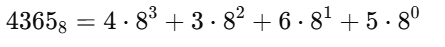
• 十进制数转换为八进制数——除R取余法
  
• 十进制数转化为二进制数
  

3.6~3.11

---

• 符号-数值形式要和二进制补码形式区分！
  符号-数值形式的最高位仅仅表示符号±，不带有权值，比如1 01在符号-数值形式下就是-1，在二进制补码形式下就是-4+1=-3
• 如何判断是否溢出？
  题目说明了是“8位”，所以8位二进制的表示范围是[-2^7,2^7-1]即[-128,127]，超出这个范围的都是溢出
• 饱和算法
  就是当上溢出时，用上界作为计算结果；下溢出时，用下界作为计算结果。
  比如计算结果是-150，那么就用-128（下界）作为结果
• “假设8位十进制数151和214以二进制补码形式存储，使用饱和算法计算151+214”
  $151{10}=(1001 1001)_2=-128+23=-105$
  $214{10}=(11010110)_2=-128+86=-42$
  $-105+(-42)=-147=-128（饱和算法）$
  PS：先分别把两个十进制数转化为二进制 并按照“二进制补码形式”求值，然后相加
• 区分“带符号数”vs“无符号数”
  比如带符号8位十进制数的表示范围[-128,127]，而无符号8位十进制数的表示范围[0,255]

3.12

---

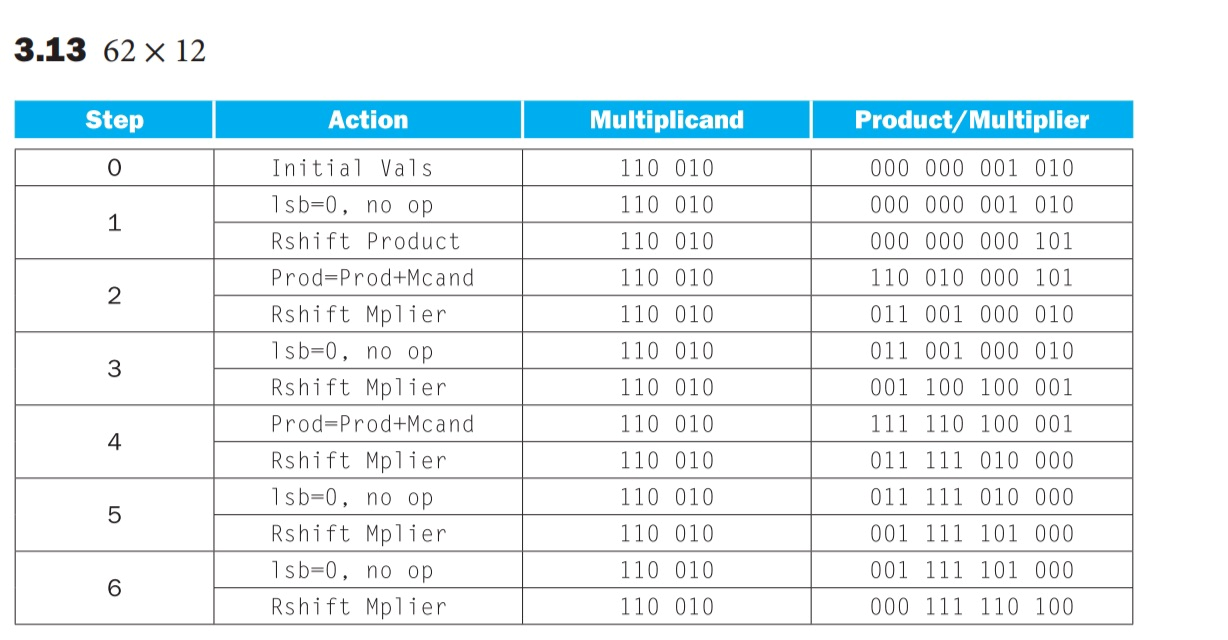
3.13

---

3.22

---

• 1+8+23的IEEE表示的浮点数中，8位的E字段，表示的是加完127后的指数！所以由IEEE的32位二进制表示转换为十进制表示时，指数要-127
  

3.23

---

• 与3.22相反，由十进制表示转化为IEEE 32位二进制表示，就要把指数**+127 **
  

3.24

---

• 3.23的双精度版本，注意双精度的偏移量是1023而不是1024，就像单精度的是127而非128！
  
• 尾数M部分是紧贴着E的最后一位写的。M的最高位就是$2^{-1}$

3.25

---

• 把十进制小数转换为二进制小数的方法
  把二进制小数的各个位上的权值写出来，比如0._ _ _ _ _ _ _ _ _，从高到低各位的权值依次是：
  0.25、0.125、0.0625、0.03125……（依次除以2）
  然后看怎么拼凑，能加出所要转换的十进制数即可

• 题目新定义的浮点数格式，并没有说明“有隐含的前导1”，所以其小数点前面是0而不是1。
  题目也没说偏移量什么的，所以不用管它
  

• 注意负数怎么用补码表示
  原码就是“符号-数值形式”，比如-2的原码是1000 0000 0010；
  补码是原码除符号位外按位取反再加一，比如-2的补码是1111 1111 1101+1=1111 1111 1110

  又比如-0.101，其原码为1.101，补码就是1.010+1=1.011（因为是尾数，所以把小数点左边的 1写到M字段的最高位）

3.27

---

• 题目说了有隐含1和偏移量，就要算上
  

• 把十进制数转换为二进制数表示的时候，一定要先把十进制数变成“小数点左边只有0”的形式，比如-1.5625要变成-0.15625，否则得到的二进制数表示不一样！
• 然后如果有前导1，就写成$±1.xx×2^n$的形式，否则就保持$±0.xx×2^n$

3.30~3.40

---

看不懂！！